

Hyperbolic Conservation Laws:
(*) A central-upwind scheme with artificial viscosity for shallow-water flows in channels.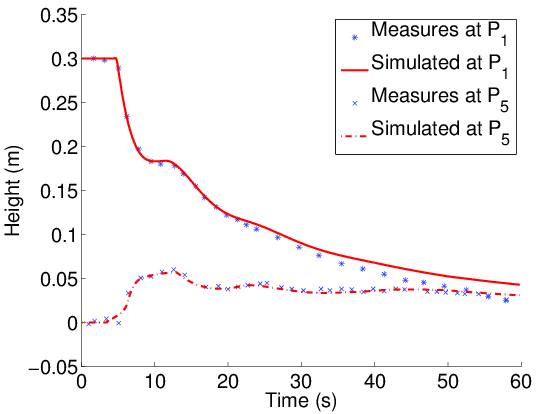

G. Hernandez-Duenas and Abdelaziz Beljadid.
Advances in Water Resources 96 (2016) 323-338.
Figure (left): Schematic of channel in numerical experiment of dam break
Figure (right): Comparison with experimental data
(*) A
Positivity Preserving
Central Scheme for Shallow Water Flows in Channels with Wet-Dry States.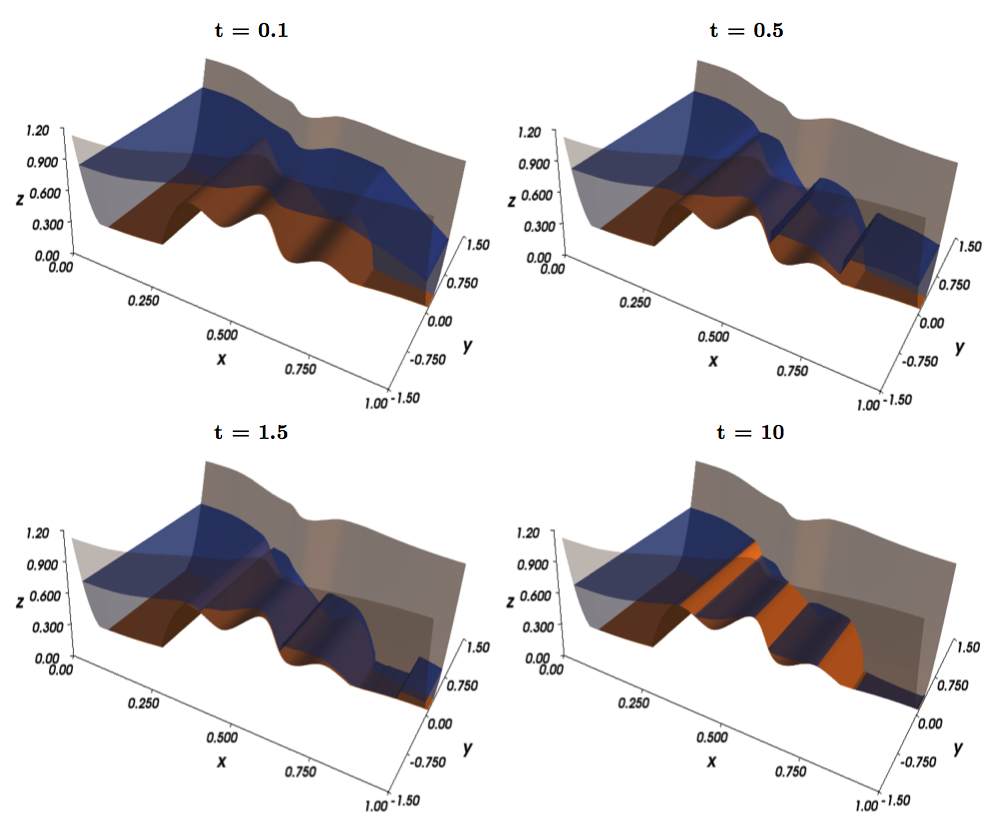
Jorge Balbás and G. Hernandez-Duenas.
ESIAM: Mathematical Modelling and Numerical Analysis (M2AN) 48 (2014) 665-696.
Figure: Dam
break simulation at different times.
Blue: Water
height. Brown: Bottom topography. Gray: Walls.
(*)
Shallow
Water Flows in Channels.
G. Hernandez-Duenas and Smadar Karni.
J. Sci. Comput. 48 (2011), no. 1-3, 190-208.
Figure: Exact and numerical steady state (discontinuous transcritical) solutions to shallow water.
(*) A
Hybrid Algorithm for the Baer-Nunziato
Model Using
the Riemann Invariants.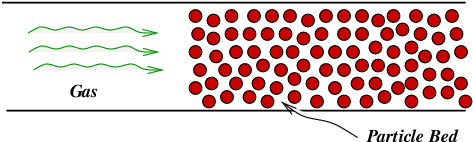
Smadar Karni and G. Hernandez-Duenas.
J Sci Comput, 45, (2010), 382-403.
Figure 1: Schematic: Gas flow
over a porous particle bed.
Semiclassical Analysis:
(*
)Algebras
of semiclassical
pseudodifferential operators associated
with Zoll-type domains in cotangent bundles 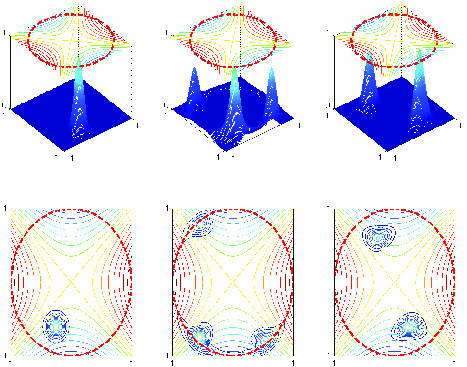
G. Hernandez-Duenas and Alejandro Uribe.
Journal of Functional Analysis, 268 no. 7 (2015), pp. 1755-1807
Figure: Propagation of a coherent state in a Zoll-type domain.
PaperAtmospheric Sciences:
(*) Stability and instability criteria for idealized precipitating hydrodynamics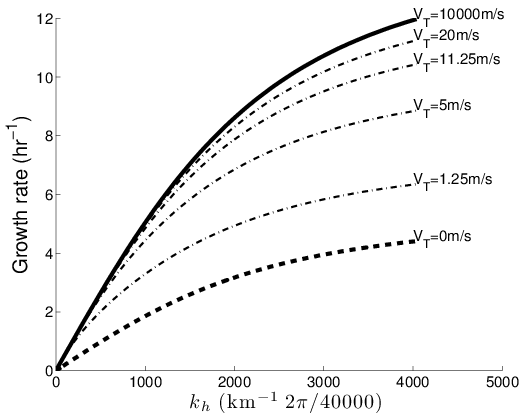
G. Hernandez-Duenas, Leslie M. Smith, and Samuel N. Stechmann.
Journal of Atmospheric Sciences, Vol 72, No. 6 (2015), pp. 2379-2393
Figure: Growth rates versus horizontal wavenumbers for different values of rainfall speed.
(*)
Minimal
models for precipitating turbulent convection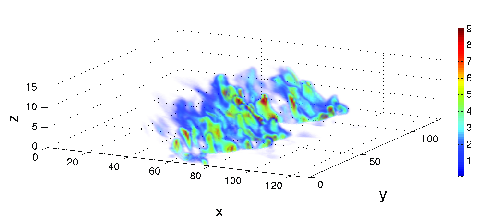
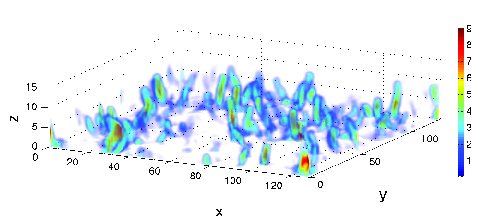
G. Hernandez-Duenas, Andrew J. Majda, Leslie M. Smith, and Samuel N. Stechmann.
Journal of Fluid Mechanics, 717 (2013), 576-611.
Figure: Contours of rain water. Scattered convection (left) versus squall lines (right).
Turbulence:
(*) Investigation of Boussinesq dynamics using intermediate models based on wave-vortical interactions.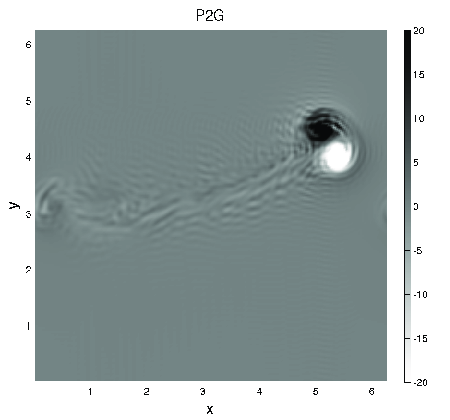
G. Hernandez-Duenas, Leslie M. Smith, and Samuel N. Stechmann
Journal of Fluid Mechanics, 747 (2014), 247-287
How to cite this article
Ph.D.Thesis (University of Michigan - Ann Arbor):
(*) Numerical Methods for Porous Media and Shallow Water Flows & An Algebra of Singular Semiclassical Pseudodifferential Operators
G. Hernandez-Duenas.
Thesis
Proceedings:
(*) A
Hybrid Scheme for Flows in Porous Media.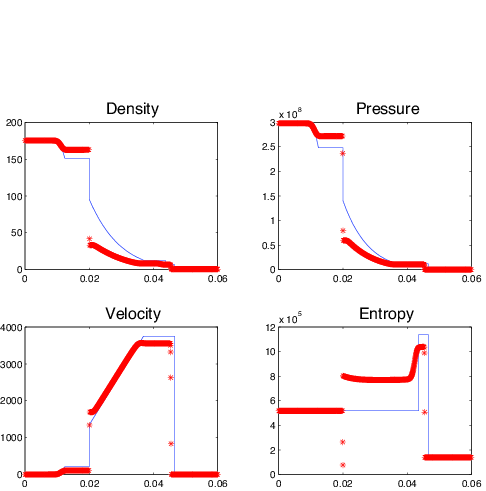
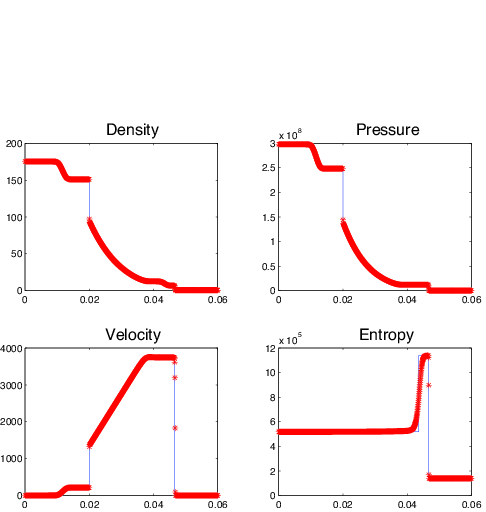
Smadar Karni and G. Hernandez-Duenas.
Hyperbolic Problems: Theory, Numerics, Applications.
Proceedings of Simposia in Applied Mathematics, Volume 67, Part 2, (2009), 715-724.
Amer. Math. Soc., Providence, RI, (2009).
How to cite this articleFigure: Computed and exact solutions in a shock-tube problem using a conservative (left) and a hybrid (right) formulation.
(*) A
Scheme for Shallow Water Flow with Area Variation.
Smadar Karni and G. Hernandez-Duenas.
American Institute of Physics.
AIP Conference Proceedings
International Conference on Numerical Analysis and Applied Mathematics
Rethymno, Crete, Greece, 18-22 September 2009. 1168 (2009), 1433-1436.