

Next: About this document ...
Up: Presentation
Previous: Scientific organization
[1]
C. Amiot, On the structure of triangulated category with finitely many
indecomposables, 27 pages, arxiv:math/0612141v1 [math.CT].
[2]
I. Assem, T. Brüstle, and R. Schiffler, Cluster-tilted algebras and
slices, 21 pages, arXiv:0707.0038v2 [math.RT].
[3]
----, Cluster-tilted algebras as trivial extensions, 14 pages,
arXiv:math/0601537 [math.RT].
[4]
----, On the Galois coverings of a cluster-tilted algebra, 21
pages, arXiv:0709.0850v1 [math.RT].
[5]
I. Assem, T. Brüstle, R. Schiffler, and G. Todorov, Cluster
categories and duplicated algebras, J. Algebra 305 (2006), no. 1,
548-561.
[6]
Ch. A. Athanasiadis, Generalized Catalan numbers, Weyl groups and
arrangements of hyperplanes, Bull. London Math. Soc. 36 (2004),
no. 3, 294-302.
[7]
----, On a refinement of the generalized Catalan numbers for Weyl
groups, Trans. Amer. Math. Soc. 357 (2005), no. 1, 179-196
(electronic).
[8]
----, On some enumerative aspects of generalized associahedra,
European J. Combin. 28 (2007), no. 4, 1208-1215.
[9]
Ch. A. Athanasiadis, Th. Brady, J. McCammond, and C. Watt, 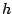 -vectors
of generalized associahedra and noncrossing partitions, Int. Math. Res. Not.
(2006), Art. ID 69705, 28.
[10]
Ch. A. Athanasiadis, Th. Brady, and C. Watt, Shellability of noncrossing
partition lattices, Proc. Amer. Math. Soc. 135 (2007), no. 4,
939-949 (electronic).
[11]
Ch. A. Athanasiadis and E. Tzanaki, On the enumeration of positive cells
in generalized cluster complexes and Catalan hyperplane arrangements, J.
Algebraic Combin. 23 (2006), no. 4, 355-375.
[12]
M. Barot, Ch. Geiss, and A. Zelevinsky, Cluster algebras of finite type
and positive symmetrizable matrices, J. London Math. Soc. (2) 73
(2006), no. 3, 545-564.
[13]
J. Bell and M. Skandera, Multicomplexes and polynomials with real zeros,
Discrete Math. 307 (2007), no. 6, 668-682.
[14]
A. Berenstein, S. Fomin, and A. Zelevinsky, Cluster algebras. III.
Upper bounds and double Bruhat cells, Duke Math. J. 126 (2005),
no. 1, 1-52.
[15]
A. Berenstein and A. Zelevinsky, Quantum cluster algebras, Adv. Math.
195 (2005), no. 2, 405-455.
[16]
N. Bergeron, Ch. Hohlweg, Lange C., and H. Thomas, Isometry classes of
generalized associahedra, 12 pages, arXiv:0709.4421 [math.CO].
[17]
D. Bessis, The dual braid monoid, Ann. Sci. École Norm. Sup. (4)
36 (2003), no. 5, 647-683.
[18]
D. Bessis and R. Corran, Non-crossing partitions of type
-vectors
of generalized associahedra and noncrossing partitions, Int. Math. Res. Not.
(2006), Art. ID 69705, 28.
[10]
Ch. A. Athanasiadis, Th. Brady, and C. Watt, Shellability of noncrossing
partition lattices, Proc. Amer. Math. Soc. 135 (2007), no. 4,
939-949 (electronic).
[11]
Ch. A. Athanasiadis and E. Tzanaki, On the enumeration of positive cells
in generalized cluster complexes and Catalan hyperplane arrangements, J.
Algebraic Combin. 23 (2006), no. 4, 355-375.
[12]
M. Barot, Ch. Geiss, and A. Zelevinsky, Cluster algebras of finite type
and positive symmetrizable matrices, J. London Math. Soc. (2) 73
(2006), no. 3, 545-564.
[13]
J. Bell and M. Skandera, Multicomplexes and polynomials with real zeros,
Discrete Math. 307 (2007), no. 6, 668-682.
[14]
A. Berenstein, S. Fomin, and A. Zelevinsky, Cluster algebras. III.
Upper bounds and double Bruhat cells, Duke Math. J. 126 (2005),
no. 1, 1-52.
[15]
A. Berenstein and A. Zelevinsky, Quantum cluster algebras, Adv. Math.
195 (2005), no. 2, 405-455.
[16]
N. Bergeron, Ch. Hohlweg, Lange C., and H. Thomas, Isometry classes of
generalized associahedra, 12 pages, arXiv:0709.4421 [math.CO].
[17]
D. Bessis, The dual braid monoid, Ann. Sci. École Norm. Sup. (4)
36 (2003), no. 5, 647-683.
[18]
D. Bessis and R. Corran, Non-crossing partitions of type 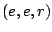 ,
Adv. Math. 202 (2006), no. 1, 1-49.
[19]
T. Bridgeland, Stability conditions on triangulated categories, 29
pages, to appear Annals of Math., math/0212237v3 [math.AG].
[20]
K. A. Brown, K. R. Goodearl, and M. Yakimov, Poisson structures on affine
spaces and flag varieties. I. Matrix affine Poisson space, Adv. Math.
206 (2006), no. 2, 567-629.
[21]
A. Buan, O. Iyama, I. Reiten, and J. Scott, Cluster structures for
2-Calabi-Yau categories and unipotent groups, 73 pages,
arXiv:math/0701557v2 [math.RT].
[22]
A. Buan, R. Marsh, M. Reineke, I. Reiten, and G. Todorov, Tilting theory
and cluster combinatorics, Adv. Math. 204 (2006), no. 2, 572-618.
[23]
A. Buan, R. Marsh, and I. Reiten, Cluster mutation via quiver
representations, 28 pages, arXiv:math/0412077v2 [math.RT].
[24]
----, Cluster-tilted algebras of finite representation type, J.
Algebra 306 (2006), no. 2, 412-431.
[25]
----, Cluster-tilted algebras, Trans. Amer. Math. Soc. 359
(2007), no. 1, 323-332 (electronic).
[26]
A. Buan, R. Marsh, I. Reiten, and G. Todorov, Clusters and seeds in
acyclic cluster algebras, 12 pages, with an appendix coauthored in addition
by P. Caldero and B. Keller, arXiv:math/0510359v3 [math.RT].
[27]
A. Buan and I. Reiten, Cluster algebras associated with extended dynkin
quivers, 6 pages, arXiv:math/0507113v1 [marth.RT].
[28]
----, From tilted to cluster-tilted algebras of dynkin type, 9 pages,
arXiv:math/0510445v1 [math.RT].
[29]
----, Acyclic quivers of finite mutation type, Int. Math. Res. Not.
(2006), Art. ID 12804, 10.
[30]
A. Buan, I. Reiten, and A. Seven, Tame concealed algebras and cluster
quivers of minimal infinite type, 16 pages, arXiv:math/0512137v2
[math.RT].
[31]
P. Caldero and B. Keller, From triangulated categories to cluster
algebras, 31 pages, to appear Inventiones Math.,
arXiv:math/0506018v2.
[32]
P. Caldero and M. Reineke, On the quiver Grassmannian in the acyclic
case, 16 pages, arXiv:math/0611074v2 [math.RT].
[33]
P. Caldero and A. Zelevinsky, Laurent expansions in cluster algebras via
quiver representations, Mosc. Math. J. 6 (2006), no. 3, 411-429.
[34]
M.P. Carr and S.L. Devadoss, Coxeter complexes and graph-associahedra,
Topology Appl. 153 (2006), no. 12, 2155-2168.
[35]
G. D. Carroll and D. Speyer, The cube recurrence, Electron. J. Combin.
11 (2004), no. 1, Research Paper 73, 31 pp. (electronic).
[36]
F. Chapoton, Enumerative properties of generalized associahedra, 15
pages, arXiv:math/0401237v1 [math.CO].
[37]
----, Enumerative properties of generalized associahedra, Sém.
Lothar. Combin. 51 (2004/05), Art. B51b, 16 pp. (electronic).
[38]
----, Functional identities for the Rogers dilogarithm associated to
cluster
,
Adv. Math. 202 (2006), no. 1, 1-49.
[19]
T. Bridgeland, Stability conditions on triangulated categories, 29
pages, to appear Annals of Math., math/0212237v3 [math.AG].
[20]
K. A. Brown, K. R. Goodearl, and M. Yakimov, Poisson structures on affine
spaces and flag varieties. I. Matrix affine Poisson space, Adv. Math.
206 (2006), no. 2, 567-629.
[21]
A. Buan, O. Iyama, I. Reiten, and J. Scott, Cluster structures for
2-Calabi-Yau categories and unipotent groups, 73 pages,
arXiv:math/0701557v2 [math.RT].
[22]
A. Buan, R. Marsh, M. Reineke, I. Reiten, and G. Todorov, Tilting theory
and cluster combinatorics, Adv. Math. 204 (2006), no. 2, 572-618.
[23]
A. Buan, R. Marsh, and I. Reiten, Cluster mutation via quiver
representations, 28 pages, arXiv:math/0412077v2 [math.RT].
[24]
----, Cluster-tilted algebras of finite representation type, J.
Algebra 306 (2006), no. 2, 412-431.
[25]
----, Cluster-tilted algebras, Trans. Amer. Math. Soc. 359
(2007), no. 1, 323-332 (electronic).
[26]
A. Buan, R. Marsh, I. Reiten, and G. Todorov, Clusters and seeds in
acyclic cluster algebras, 12 pages, with an appendix coauthored in addition
by P. Caldero and B. Keller, arXiv:math/0510359v3 [math.RT].
[27]
A. Buan and I. Reiten, Cluster algebras associated with extended dynkin
quivers, 6 pages, arXiv:math/0507113v1 [marth.RT].
[28]
----, From tilted to cluster-tilted algebras of dynkin type, 9 pages,
arXiv:math/0510445v1 [math.RT].
[29]
----, Acyclic quivers of finite mutation type, Int. Math. Res. Not.
(2006), Art. ID 12804, 10.
[30]
A. Buan, I. Reiten, and A. Seven, Tame concealed algebras and cluster
quivers of minimal infinite type, 16 pages, arXiv:math/0512137v2
[math.RT].
[31]
P. Caldero and B. Keller, From triangulated categories to cluster
algebras, 31 pages, to appear Inventiones Math.,
arXiv:math/0506018v2.
[32]
P. Caldero and M. Reineke, On the quiver Grassmannian in the acyclic
case, 16 pages, arXiv:math/0611074v2 [math.RT].
[33]
P. Caldero and A. Zelevinsky, Laurent expansions in cluster algebras via
quiver representations, Mosc. Math. J. 6 (2006), no. 3, 411-429.
[34]
M.P. Carr and S.L. Devadoss, Coxeter complexes and graph-associahedra,
Topology Appl. 153 (2006), no. 12, 2155-2168.
[35]
G. D. Carroll and D. Speyer, The cube recurrence, Electron. J. Combin.
11 (2004), no. 1, Research Paper 73, 31 pp. (electronic).
[36]
F. Chapoton, Enumerative properties of generalized associahedra, 15
pages, arXiv:math/0401237v1 [math.CO].
[37]
----, Enumerative properties of generalized associahedra, Sém.
Lothar. Combin. 51 (2004/05), Art. B51b, 16 pp. (electronic).
[38]
----, Functional identities for the Rogers dilogarithm associated to
cluster 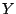 -systems, Bull. London Math. Soc. 37 (2005), no. 5,
755-760.
[39]
----, Une base symétrique de l'algèbre des coinvariants
quasi-symétriques, Electron. J. Combin. 12 (2005), Note 16, 7 pp.
(electronic).
[40]
F. Chapoton, S. Fomin, and A. Zelevinsky, Polytopal realizations of
generalized associahedra, Canad. Math. Bull. 45 (2002), no. 4,
537-566, Dedicated to Robert V. Moody.
[41]
L. O. Chekhov and V. V. Fock, Quantum Teichmüller spaces, Teoret.
Mat. Fiz. 120 (1999), no. 3, 511-528, arXiv: math/9908165
[math.QA].
[42]
Suhyoung Choi and W. Goldman, The deformation spaces of convex
-systems, Bull. London Math. Soc. 37 (2005), no. 5,
755-760.
[39]
----, Une base symétrique de l'algèbre des coinvariants
quasi-symétriques, Electron. J. Combin. 12 (2005), Note 16, 7 pp.
(electronic).
[40]
F. Chapoton, S. Fomin, and A. Zelevinsky, Polytopal realizations of
generalized associahedra, Canad. Math. Bull. 45 (2002), no. 4,
537-566, Dedicated to Robert V. Moody.
[41]
L. O. Chekhov and V. V. Fock, Quantum Teichmüller spaces, Teoret.
Mat. Fiz. 120 (1999), no. 3, 511-528, arXiv: math/9908165
[math.QA].
[42]
Suhyoung Choi and W. Goldman, The deformation spaces of convex
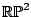 -structures on 2-orbifolds, Amer. J. Math. 127
(2005), no. 5, 1019-1102.
[43]
R. Dehy and B. Keller, Index and h-vector, 10 pages,
arXiv:0709.0882v1 [math.RT].
[44]
H. Derksen, J. Weyman, and A. Zelevinsky, Quivers with potentials and
their representations I: Mutations, 58 pages, arXiv:0704.0649v3
[math.RA].
[45]
B. Drake, S. Gerrish, and M. Skandera, Two new criteria for comparison in
the Bruhat order, Electron. J. Combin. 11 (2004), no. 1, Note 6,
4 pp. (electronic).
[46]
----, Monomial nonnegativity and the Bruhat order, Electron. J.
Combin. 11 (2004/06), no. 2, Research Paper 18, 5 pp. (electronic).
[47]
V. Fock and A Goncharov, Cluster ensembles, quantization and the
dilogarithm, arXiv:math/0311245 [math.AG].
[48]
V. Fock and A. Goncharov, The quantum dilogarithm and representations
quantized cluster varieties, 58 pages, arXiv: math/0702397v5
[math.QA].
[49]
----, Cluster X-varieties, amalgamation and Poisson-Lie groups,
Algebraic geometry and number theory,, Progr. Math., vol. 253, Birkhäuser
Boston, Boston, MA, 2006, Volume dedicated to V. Drinfeld, pp. 27-68.
[50]
----, Moduli spaces of local systems and higher Teichmüller
theory, Publ. Math. Inst. Hautes Études Sci. (2006), no. 103, 1-211.
[51]
----, Moduli spaces of convex projective structures on surfaces, Adv.
Math. 208 (2007), no. 1, 249-273.
[52]
S. Fomin and N. Reading, Root systems and generalized associahedra,
Lecture notes for IAS/Park-City 2004, 69 pages, arXiv:math.CO/0505518v2
[math.CO].
[53]
----, Generalized cluster complexes and Coxeter combinatorics, Int.
Math. Res. Not. (2005), no. 44, 2709-2757.
[54]
S. Fomin, M. Shapiro, and D. Thurston, Cluster algebras and triangulated
surfaces. Part I: Cluster complexes., 56 pages, math.RA/0608367v3
[math.RA].
[55]
S. Fomin and A. Zelevinsky, Cluster algebras. I. Foundations, J.
Amer. Math. Soc. 15 (2002), no. 2, 497-529 (electronic),
arXiv:math/0104151v1 [math.RT].
[56]
----, The Laurent phenomenon, Adv. in Appl. Math. 28
(2002), no. 2, 119-144.
[57]
----, Cluster algebras. II. Finite type classification, Invent.
Math. 154 (2003), no. 1, 63-121.
[58]
----,
-structures on 2-orbifolds, Amer. J. Math. 127
(2005), no. 5, 1019-1102.
[43]
R. Dehy and B. Keller, Index and h-vector, 10 pages,
arXiv:0709.0882v1 [math.RT].
[44]
H. Derksen, J. Weyman, and A. Zelevinsky, Quivers with potentials and
their representations I: Mutations, 58 pages, arXiv:0704.0649v3
[math.RA].
[45]
B. Drake, S. Gerrish, and M. Skandera, Two new criteria for comparison in
the Bruhat order, Electron. J. Combin. 11 (2004), no. 1, Note 6,
4 pp. (electronic).
[46]
----, Monomial nonnegativity and the Bruhat order, Electron. J.
Combin. 11 (2004/06), no. 2, Research Paper 18, 5 pp. (electronic).
[47]
V. Fock and A Goncharov, Cluster ensembles, quantization and the
dilogarithm, arXiv:math/0311245 [math.AG].
[48]
V. Fock and A. Goncharov, The quantum dilogarithm and representations
quantized cluster varieties, 58 pages, arXiv: math/0702397v5
[math.QA].
[49]
----, Cluster X-varieties, amalgamation and Poisson-Lie groups,
Algebraic geometry and number theory,, Progr. Math., vol. 253, Birkhäuser
Boston, Boston, MA, 2006, Volume dedicated to V. Drinfeld, pp. 27-68.
[50]
----, Moduli spaces of local systems and higher Teichmüller
theory, Publ. Math. Inst. Hautes Études Sci. (2006), no. 103, 1-211.
[51]
----, Moduli spaces of convex projective structures on surfaces, Adv.
Math. 208 (2007), no. 1, 249-273.
[52]
S. Fomin and N. Reading, Root systems and generalized associahedra,
Lecture notes for IAS/Park-City 2004, 69 pages, arXiv:math.CO/0505518v2
[math.CO].
[53]
----, Generalized cluster complexes and Coxeter combinatorics, Int.
Math. Res. Not. (2005), no. 44, 2709-2757.
[54]
S. Fomin, M. Shapiro, and D. Thurston, Cluster algebras and triangulated
surfaces. Part I: Cluster complexes., 56 pages, math.RA/0608367v3
[math.RA].
[55]
S. Fomin and A. Zelevinsky, Cluster algebras. I. Foundations, J.
Amer. Math. Soc. 15 (2002), no. 2, 497-529 (electronic),
arXiv:math/0104151v1 [math.RT].
[56]
----, The Laurent phenomenon, Adv. in Appl. Math. 28
(2002), no. 2, 119-144.
[57]
----, Cluster algebras. II. Finite type classification, Invent.
Math. 154 (2003), no. 1, 63-121.
[58]
----, 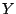 -systems and generalized associahedra, Ann. of Math. (2)
158 (2003), no. 3, 977-1018.
[59]
----, Cluster algebras. IV. Coefficients, Compos. Math.
143 (2007), no. 1, 112-164.
[60]
Ch. Fu and B. Keller, On cluster algebras with coefficients and
2-calabi-yau categories, 24 pages, arXiv:0710.3152v1 [math.RT].
[61]
Ch. Geiss, B. Leclerc, and J. Schröer, Auslander algebras and initial
seeds for cluster algebras, 23 pages, to appear J. London Math. Soc.,
arXiv:math/0506405v4 [math.RT].
[62]
----, Partial flag varieties and preprojective algebras, 42 pages, to
appear in Annales de l'Institut Fourier, arXiv:math/0609138v3
[math.RT].
[63]
----, Rigid modules over preprojective algebras II: The
Kac-Moody case, 49 pages, arXiv:math/0703039v1 [math.RT].
[64]
----, Semicanonical bases and preprojective algebras II: A
multiplication formula, 22 pages, to appear in Compositio Math.,
arXiv:math/0509483v3 [math.RT].
[65]
----, Semicanonical bases and preprojective algebras, Ann. Sci.
École Norm. Sup. (4) 38 (2005), no. 2, 193-253.
[66]
----, Rigid modules over preprojective algebras, Invent. Math.
165 (2006), no. 3, 589-632.
[67]
M. Gekhtman, M. Shapiro, and A. Vainshtein, Cluster algebras and
Poisson geometry, Mosc. Math. J. 3 (2003), no. 3, 899-934, 1199,
{Dedicated to Vladimir Igorevich Arnold on the occasion of his 65th
birthday}.
[68]
----, Cluster algebras and Weil-Petersson forms, Duke Math. J.
127 (2005), no. 2, 291-311.
[69]
W. Goldman, Convex real projective structures on compact surfaces, J.
Differential Geom. 31 (1990), no. 3, 791-845.
[70]
A. Goncharov, Pentagon relation for the quantum dilogarithm and quantized
-systems and generalized associahedra, Ann. of Math. (2)
158 (2003), no. 3, 977-1018.
[59]
----, Cluster algebras. IV. Coefficients, Compos. Math.
143 (2007), no. 1, 112-164.
[60]
Ch. Fu and B. Keller, On cluster algebras with coefficients and
2-calabi-yau categories, 24 pages, arXiv:0710.3152v1 [math.RT].
[61]
Ch. Geiss, B. Leclerc, and J. Schröer, Auslander algebras and initial
seeds for cluster algebras, 23 pages, to appear J. London Math. Soc.,
arXiv:math/0506405v4 [math.RT].
[62]
----, Partial flag varieties and preprojective algebras, 42 pages, to
appear in Annales de l'Institut Fourier, arXiv:math/0609138v3
[math.RT].
[63]
----, Rigid modules over preprojective algebras II: The
Kac-Moody case, 49 pages, arXiv:math/0703039v1 [math.RT].
[64]
----, Semicanonical bases and preprojective algebras II: A
multiplication formula, 22 pages, to appear in Compositio Math.,
arXiv:math/0509483v3 [math.RT].
[65]
----, Semicanonical bases and preprojective algebras, Ann. Sci.
École Norm. Sup. (4) 38 (2005), no. 2, 193-253.
[66]
----, Rigid modules over preprojective algebras, Invent. Math.
165 (2006), no. 3, 589-632.
[67]
M. Gekhtman, M. Shapiro, and A. Vainshtein, Cluster algebras and
Poisson geometry, Mosc. Math. J. 3 (2003), no. 3, 899-934, 1199,
{Dedicated to Vladimir Igorevich Arnold on the occasion of his 65th
birthday}.
[68]
----, Cluster algebras and Weil-Petersson forms, Duke Math. J.
127 (2005), no. 2, 291-311.
[69]
W. Goldman, Convex real projective structures on compact surfaces, J.
Differential Geom. 31 (1990), no. 3, 791-845.
[70]
A. Goncharov, Pentagon relation for the quantum dilogarithm and quantized
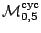 , to appear in Progress in Mathematics
volume (Birkhauser) dedicated to the memory of Alexander Reznikov,
arXiv/0704.405v2 [math.QA].
[71]
N. J. Hitchin, Lie groups and Teichmüller space, Topology
31 (1992), no. 3, 449-473.
[72]
Th. Holm and P. Jørgensen, Cluster categories and selfinjective
algebras: type A, 18 pages, arXiv:math/0610728v1 [math.RT].
[73]
----, Cluster categories and selfinjective algebras: type D, 21
pages, arXiv:math/0612451v1 [math.RT].
[74]
O. Iyama and I. Reiten, Fomin-Zelevinsky mutation and tilting modules
over Calabi-Yau algebras, 53 pages, to appear in Amer. J. Math,
arXiv:math/0605136v3 [math.RT].
[75]
R. M. Kashaev, Quantization of Teichmüller spaces and the quantum
dilogarithm, Lett. Math. Phys. 43 (1998), no. 2, 105-115,
arXiv:math/9706018 [math.QA].
[76]
B. Keller, On triangulated orbit categories, Doc. Math. 10
(2005), 551-581 (electronic).
[77]
B. Keller and I. Reiten, Acyclic calabi-yau categories, 16 pages,
arXiv:math/0610594v2 [math.RT].
[78]
----, Cluster-tilted algebras are Gorenstein and stably
Calabi-Yau, Adv. Math. 211 (2007), no. 1, 123-151.
[79]
M. Kogan and A. Zelevinsky, On symplectic leaves and integrable systems
in standard complex semisimple Poisson-Lie groups, Int. Math. Res. Not.
(2002), no. 32, 1685-1702.
[80]
M. Kontsevich, Donaldson-thomas invariants, Notes for Mathematische
Arbeitstagung, June 22-28 at MPIM Bonn,
www.mpim-bonn.mpg.de/preprints/send?bid=3352.
[81]
C. Krattenthaler, The
, to appear in Progress in Mathematics
volume (Birkhauser) dedicated to the memory of Alexander Reznikov,
arXiv/0704.405v2 [math.QA].
[71]
N. J. Hitchin, Lie groups and Teichmüller space, Topology
31 (1992), no. 3, 449-473.
[72]
Th. Holm and P. Jørgensen, Cluster categories and selfinjective
algebras: type A, 18 pages, arXiv:math/0610728v1 [math.RT].
[73]
----, Cluster categories and selfinjective algebras: type D, 21
pages, arXiv:math/0612451v1 [math.RT].
[74]
O. Iyama and I. Reiten, Fomin-Zelevinsky mutation and tilting modules
over Calabi-Yau algebras, 53 pages, to appear in Amer. J. Math,
arXiv:math/0605136v3 [math.RT].
[75]
R. M. Kashaev, Quantization of Teichmüller spaces and the quantum
dilogarithm, Lett. Math. Phys. 43 (1998), no. 2, 105-115,
arXiv:math/9706018 [math.QA].
[76]
B. Keller, On triangulated orbit categories, Doc. Math. 10
(2005), 551-581 (electronic).
[77]
B. Keller and I. Reiten, Acyclic calabi-yau categories, 16 pages,
arXiv:math/0610594v2 [math.RT].
[78]
----, Cluster-tilted algebras are Gorenstein and stably
Calabi-Yau, Adv. Math. 211 (2007), no. 1, 123-151.
[79]
M. Kogan and A. Zelevinsky, On symplectic leaves and integrable systems
in standard complex semisimple Poisson-Lie groups, Int. Math. Res. Not.
(2002), no. 32, 1685-1702.
[80]
M. Kontsevich, Donaldson-thomas invariants, Notes for Mathematische
Arbeitstagung, June 22-28 at MPIM Bonn,
www.mpim-bonn.mpg.de/preprints/send?bid=3352.
[81]
C. Krattenthaler, The 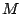 -triangle of generalised non-crossing
partitions for the types
-triangle of generalised non-crossing
partitions for the types  and
and  , Sém. Lothar. Combin.
54 (2005/06), Art. B541, 34 pp. (electronic).
[82]
Th. Lam and L. Williams, Total positivity for cominuscule
Grassmannians, 39 pages, arXiv:0710.2932 [math.CO].
[83]
G. Lusztig, A survey of total positivity, 8 pages,
arXiv:0705.3842v1 [math.RT].
[84]
----, Total positivity in reductive groups, Lie theory and geometry,
Progr. Math., vol. 123, Birkhäuser Boston, Boston, MA, 1994, pp. 531-568.
[85]
----, Introduction to total positivity, Positivity in Lie theory:
open problems, de Gruyter Exp. Math., vol. 26, de Gruyter, Berlin, 1998,
pp. 133-145.
[86]
----, Semicanonical bases arising from enveloping algebras, Adv.
Math. 151 (2000), no. 2, 129-139.
[87]
R. Marsh, M. Reineke, and A. Zelevinsky, Generalized associahedra via
quiver representations, Trans. Amer. Math. Soc. 355 (2003), no. 10,
4171-4186 (electronic).
[88]
J. McCammond, Noncrossing partitions in surprising locations, Amer.
Math. Monthly 113 (2006), no. 7, 598-610.
[89]
G. Musiker and J. Propp, Combinatorial interpretations for rank-two
cluster algebras of affine type, Electron. J. Combin. 14 (2007),
no. 1, Research Paper 15, 23 pp. (electronic).
[90]
Y. Palu, Cluster characters for triangulated 2-Calabi-Yau
categories, 21 pages, arXiv:math/0703540v2 [math.RT].
[91]
D. I. Panyushev, The poset of positive roots and its relatives, J.
Algebraic Combin. 23 (2006), no. 1, 79-101.
[92]
R. C. Penner, The decorated Teichmüller space of punctured surfaces,
Comm. Math. Phys. 113 (1987), no. 2, 299-339.
[93]
A. Postnikov, D. Speyer, and L. Williams, Matching polytopes, toric
geometry, and the non-negative part of the grassmannian, 26 pages,
arXiv:0706.2501 [math.AG].
[94]
N. Reading, Lattice congruences of the weak order, Order 21
(2004), no. 4, 315-344 (2005).
[95]
----, Lattice congruences, fans and Hopf algebras, J. Combin.
Theory Ser. A 110 (2005), no. 2, 237-273.
[96]
----, Cambrian lattices, Adv. Math. 205 (2006), no. 2,
313-353.
[97]
V. Reiner and V. Welker, On the Charney-Davis and Neggers-Stanley
conjectures, J. Combin. Theory Ser. A 109 (2005), no. 2, 247-280.
[98]
C.M. Ringel, The self-injective cluster tilted algebras, 5 pages,
arXiv:0705.3903 [math.CO].
[99]
----, some remarks concerning tilting modules and tilted algebras.
origin. relevance. future., An appendix to the Handbook of Tilting Theory,
arXiv:math/0605712 [math.RT].
[100]
N. Sandman, A type-B Tamari poset, Discrete Appl. Math. 143
(2004), no. 1-3, 110-122.
[101]
A. I. Seven, Recognizing cluster algebras of finite type, Electron. J.
Combin. 14 (2007), no. 1, Research Paper 3, 35 pp. (electronic),
arXiv:math/0406545v2 [math.CO].
[102]
R. Simion, A type-B associahedron, Adv. in Appl. Math. 30
(2003), no. 1-2, 2-25, Formal power series and algebraic combinatorics
(Scottsdale, AZ, 2001).
[103]
D. Speyer and L. Williams, The tropical totally positive Grassmannian,
J. Algebraic Combin. 22 (2005), no. 2, 189-210.
[104]
D. E. Speyer, Perfect matchings and the octahedron recurrence, J.
Algebraic Combin. 25 (2007), no. 3, 309-348.
[105]
G. Tabuada, On the structure of Calabi-Yau categories with a cluster
tilting subcategory, Doc. Math. 12 (2007), 193-213 (electronic).
[106]
J. Teschner, On the relation between quantum Liouville theory and the
quantized Teichmüller spaces, Proceedings of 6th International Workshop
on Conformal Field Theory and Integrable Models, vol. 19, 2004, pp. 459-477.
[107]
H. Thomas, Tamari lattices and noncrossing partitions in type
, Sém. Lothar. Combin.
54 (2005/06), Art. B541, 34 pp. (electronic).
[82]
Th. Lam and L. Williams, Total positivity for cominuscule
Grassmannians, 39 pages, arXiv:0710.2932 [math.CO].
[83]
G. Lusztig, A survey of total positivity, 8 pages,
arXiv:0705.3842v1 [math.RT].
[84]
----, Total positivity in reductive groups, Lie theory and geometry,
Progr. Math., vol. 123, Birkhäuser Boston, Boston, MA, 1994, pp. 531-568.
[85]
----, Introduction to total positivity, Positivity in Lie theory:
open problems, de Gruyter Exp. Math., vol. 26, de Gruyter, Berlin, 1998,
pp. 133-145.
[86]
----, Semicanonical bases arising from enveloping algebras, Adv.
Math. 151 (2000), no. 2, 129-139.
[87]
R. Marsh, M. Reineke, and A. Zelevinsky, Generalized associahedra via
quiver representations, Trans. Amer. Math. Soc. 355 (2003), no. 10,
4171-4186 (electronic).
[88]
J. McCammond, Noncrossing partitions in surprising locations, Amer.
Math. Monthly 113 (2006), no. 7, 598-610.
[89]
G. Musiker and J. Propp, Combinatorial interpretations for rank-two
cluster algebras of affine type, Electron. J. Combin. 14 (2007),
no. 1, Research Paper 15, 23 pp. (electronic).
[90]
Y. Palu, Cluster characters for triangulated 2-Calabi-Yau
categories, 21 pages, arXiv:math/0703540v2 [math.RT].
[91]
D. I. Panyushev, The poset of positive roots and its relatives, J.
Algebraic Combin. 23 (2006), no. 1, 79-101.
[92]
R. C. Penner, The decorated Teichmüller space of punctured surfaces,
Comm. Math. Phys. 113 (1987), no. 2, 299-339.
[93]
A. Postnikov, D. Speyer, and L. Williams, Matching polytopes, toric
geometry, and the non-negative part of the grassmannian, 26 pages,
arXiv:0706.2501 [math.AG].
[94]
N. Reading, Lattice congruences of the weak order, Order 21
(2004), no. 4, 315-344 (2005).
[95]
----, Lattice congruences, fans and Hopf algebras, J. Combin.
Theory Ser. A 110 (2005), no. 2, 237-273.
[96]
----, Cambrian lattices, Adv. Math. 205 (2006), no. 2,
313-353.
[97]
V. Reiner and V. Welker, On the Charney-Davis and Neggers-Stanley
conjectures, J. Combin. Theory Ser. A 109 (2005), no. 2, 247-280.
[98]
C.M. Ringel, The self-injective cluster tilted algebras, 5 pages,
arXiv:0705.3903 [math.CO].
[99]
----, some remarks concerning tilting modules and tilted algebras.
origin. relevance. future., An appendix to the Handbook of Tilting Theory,
arXiv:math/0605712 [math.RT].
[100]
N. Sandman, A type-B Tamari poset, Discrete Appl. Math. 143
(2004), no. 1-3, 110-122.
[101]
A. I. Seven, Recognizing cluster algebras of finite type, Electron. J.
Combin. 14 (2007), no. 1, Research Paper 3, 35 pp. (electronic),
arXiv:math/0406545v2 [math.CO].
[102]
R. Simion, A type-B associahedron, Adv. in Appl. Math. 30
(2003), no. 1-2, 2-25, Formal power series and algebraic combinatorics
(Scottsdale, AZ, 2001).
[103]
D. Speyer and L. Williams, The tropical totally positive Grassmannian,
J. Algebraic Combin. 22 (2005), no. 2, 189-210.
[104]
D. E. Speyer, Perfect matchings and the octahedron recurrence, J.
Algebraic Combin. 25 (2007), no. 3, 309-348.
[105]
G. Tabuada, On the structure of Calabi-Yau categories with a cluster
tilting subcategory, Doc. Math. 12 (2007), 193-213 (electronic).
[106]
J. Teschner, On the relation between quantum Liouville theory and the
quantized Teichmüller spaces, Proceedings of 6th International Workshop
on Conformal Field Theory and Integrable Models, vol. 19, 2004, pp. 459-477.
[107]
H. Thomas, Tamari lattices and noncrossing partitions in type 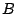 ,
Discrete Math. 306 (2006), no. 21, 2711-2723.
[108]
W. Thurston, The geometry and topology of three-manifolds, Princeton
University notes, http://www.msri.org/publications/books/gt3m.
[109]
E. Tzanaki, Polygon dissections and some generalizations of cluster
complexes, J. Combin. Theory Ser. A 113 (2006), no. 6, 1189-1198.
[110]
B. Webster and M. Yakimov, A Deodhar type stratification on the double
flag variety, 21 pages, arXiv:math/0607374 [math.SG].
[111]
L. Williams, Shelling totally nonnegative flag varieties, 21 pages,
math.RT/0509129 [math.RT].
[112]
A. Zelevinsky, Nested complexes and their polyhedral realizations, Pure
Appl. Math. Q. 2 (2006), no. 3, 655-671, arXiv:math/0507277
[math.CO].
[113]
Bin Zhu, Generalized cluster complexes via quiver representations, 20
pages, to appear J. Algebraic Comb., arXiv:math/0607155v5 [math.RT].
[114]
----, Preprojective cluster variables of acyclic cluster algebras, 18
pages, arXiv:math/0511706v3 [math.RT].
[115]
----, Applications of BGP-reflection functors: isomorphisms for
cluster algebras, Sci. China Ser. A 49 (2006), no. 12, 1839-1854.
[116]
----, Equivalences between cluster categories, J. Algebra
304 (2006), no. 2, 832-850.
[117]
----, BGP-reflection functors and cluster combinatorics, J. Pure
Appl. Algebra 209 (2007), no. 2, 497-506.
,
Discrete Math. 306 (2006), no. 21, 2711-2723.
[108]
W. Thurston, The geometry and topology of three-manifolds, Princeton
University notes, http://www.msri.org/publications/books/gt3m.
[109]
E. Tzanaki, Polygon dissections and some generalizations of cluster
complexes, J. Combin. Theory Ser. A 113 (2006), no. 6, 1189-1198.
[110]
B. Webster and M. Yakimov, A Deodhar type stratification on the double
flag variety, 21 pages, arXiv:math/0607374 [math.SG].
[111]
L. Williams, Shelling totally nonnegative flag varieties, 21 pages,
math.RT/0509129 [math.RT].
[112]
A. Zelevinsky, Nested complexes and their polyhedral realizations, Pure
Appl. Math. Q. 2 (2006), no. 3, 655-671, arXiv:math/0507277
[math.CO].
[113]
Bin Zhu, Generalized cluster complexes via quiver representations, 20
pages, to appear J. Algebraic Comb., arXiv:math/0607155v5 [math.RT].
[114]
----, Preprojective cluster variables of acyclic cluster algebras, 18
pages, arXiv:math/0511706v3 [math.RT].
[115]
----, Applications of BGP-reflection functors: isomorphisms for
cluster algebras, Sci. China Ser. A 49 (2006), no. 12, 1839-1854.
[116]
----, Equivalences between cluster categories, J. Algebra
304 (2006), no. 2, 832-850.
[117]
----, BGP-reflection functors and cluster combinatorics, J. Pure
Appl. Algebra 209 (2007), no. 2, 497-506.


Next: About this document ...
Up: Presentation
Previous: Scientific organization
![]()
![]()
![]()