El teorema de Barbier

Dado un conjunto \(K\) en el plano que es compacto, estríctamente convexo y tiene frontera suave, su ancho en la dirección \(u\) es la distancia entre las dos líneas perpendiculares a la dirección \(u\) que son tangentes a \(K\), atrapando a \(K\) entre las dos.

Teorema de Barbier. Si el ancho del convexo \(K\) es constante, digamos \(d\) en todas las direcciones, el perimetro de \(K\) es \(\pi d\).

El teorema de Barbier es consecuencia inmediata de la fórmula de Cauchy:

Fórmula de Cauchy para el perímetro. Sea \(u(\theta) = (\cos \theta, \sin \theta)\) y sea \(a(u)\) el ancho del convexo \(K\) en la dirección \(u\). Entonces el perímetro de \(K\) es \(\int_0^\pi a(u(\theta)) \; d\theta\).

Demostración. Sea \(h\) la función de soporte de \(K\), es decir, \(h(\theta)\) es la distancia desde el origen hasta la línea tangente a \(K\) perpendicular a la dirección \(u(\theta)\). (Más precisamente, \(h(\theta) = \sup_{x \in K} x \cdot u(\theta)\).) El punto de tangencia de esa tangente es de la forma \(x(\theta) = h(\theta) u(\theta) + f(\theta) u(\theta)^\perp\) para alguna función \(f\) (ver figura), donde \(u(\theta)^\perp := (- \sin \theta, cos \theta)\). Esta función \(x : [0, 2\pi] \to \mathbb{R}^2\) es una parametrización de la frontera de \(K\).

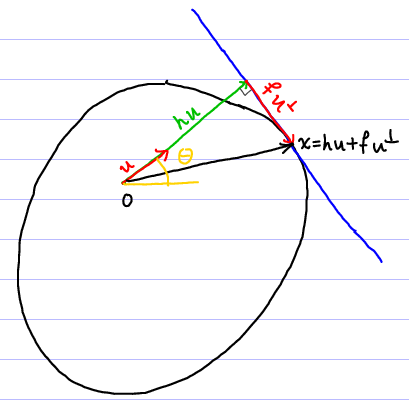
Derivando con respecto a \(\theta\) obtenemos (de ahora en adelante dejamos de escribir el argumento \(\theta\) de la funciones): \[ x' = h'u + hu' + f'u^\perp + f(u^\perp)' = (h'-f)u + (h+f') u^\perp, \] donde usamos que \(u' = u^\perp\) y \((u^\perp)' = -u\). Como el vector tangente \(x'\) debe ser paralelo a \(u^\perp\), concluímos que \(f = h'\), así que obtenemos la parametrización \(x = hu + h'u^\perp\) y para el vector tangente obtenemos \(x'=(h+h'') u^\perp\). Como consecuencia de la convexidad de \(K\), \(h+h'' \ge 0\).

Ahora podemos calcular el perímetro: \[ \int_0^{2\pi} \left| x' \right| = \int_0^{2\pi} (h+h'') = \int_0^{2\pi} h = \int_0^{\pi} a, \] donde usamos que \(\int_0^{2\pi} h'' = h'(2\pi) - h'(0) = 0\) y que \(a(\theta) = h(\theta) + h(\theta + \pi)\).