Tarea 2
Álgebra Moderna I
- Si
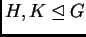 ,
, 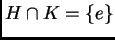 y
y 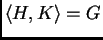 , muestra que
, muestra que 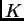 es
isomorfo a
es
isomorfo a 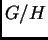 .
.
- Sea
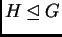 tal que
tal que ![$ [G:H]=p$](imagenes/img7.png) (
(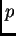 primo). Muestra que si
primo). Muestra que si
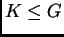 no está contenido en
no está contenido en 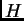 entonces
entonces 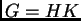 y
y
![$ [K:K\cap
H]=p$](imagenes/img12.png) .
.
- Si
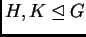 con
con 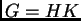 , muestra que
, muestra que
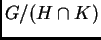 es
isomorfo a
es
isomorfo a
 .
.
- Si
![$ \xymatrix{\mathcal{S}:\;\;1\ar[r]&G'\ar[r]^f&G\ar[r]^g&G''\ar[r]&1}$](imagenes/img15.png) es una sucesión de morfismos de grupos, decimos que
es una sucesión de morfismos de grupos, decimos que
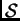 es exacta si
es exacta si 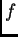 es inyectiva,
es inyectiva, 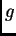 es
suprayectiva y
es
suprayectiva y
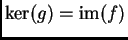 . Muestra lo siguiente:
. Muestra lo siguiente:
-
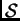 es exacta si y sólo si existe
es exacta si y sólo si existe 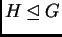 y un
diagrama conmutativo:
donde
y un
diagrama conmutativo:
donde  y
y 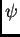 son isomorfismos.
son isomorfismos.
- Si
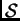 es una sucesión exacta con
es una sucesión exacta con 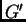 y
y 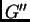 grupos
finitamente generados entonces
grupos
finitamente generados entonces 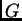 es finitamente generado.
es finitamente generado.
- Si
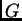 es un grupo y
es una cadena de subgrupos de
es un grupo y
es una cadena de subgrupos de 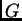 , decimos que
, decimos que
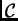 es
una cadena normal de
es
una cadena normal de 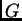 , si
, si
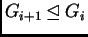 para toda
para toda 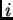 . Si
. Si
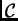 es una cadena normal de
es una cadena normal de 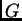 , decimos que
, decimos que
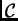 es abeliana (resp. cíclica) si
es abeliana (resp. cíclica) si
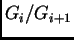 es un grupo abeliano (resp. cíclico) para toda
es un grupo abeliano (resp. cíclico) para toda 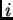 .
.
- Muestra que si
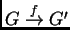 es un morfismo de grupos y
es un morfismo de grupos y
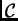 es una cadena abeliana (resp. cíclica) de
es una cadena abeliana (resp. cíclica) de 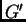 , entonces
, entonces
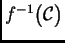 es una cadena abeliana (resp. cíclica)
de
es una cadena abeliana (resp. cíclica)
de 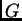 .
.
- Muestra que si
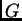 es un grupo y
es un grupo y 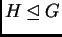 , entonces
, entonces 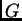 es
soluble (es decir,
es
soluble (es decir, 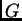 tiene una cadena abeliana con
tiene una cadena abeliana con 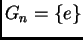 ) si
y sólo si
) si
y sólo si 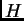 y
y 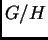 son solubles.
son solubles.
- Si
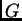 es un grupo abeliano finito y
es un grupo abeliano finito y 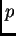 es número primo que
divide al orden de
es número primo que
divide al orden de 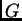 , entonces
, entonces 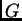 tiene un elemento de orden
tiene un elemento de orden 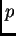 .
.
![$ \xymatrix{\mathcal{S}:\;\;1\ar[r]&G'\ar[r]^f&G\ar[r]^g&G''\ar[r]&1}$](imagenes/img15.png) es una sucesión de morfismos de grupos, decimos que
es una sucesión de morfismos de grupos, decimos que
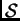 es exacta si y sólo si existe
es exacta si y sólo si existe 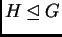 y un
diagrama conmutativo:
donde
y un
diagrama conmutativo:
donde![$\displaystyle \xymatrix{1\ar[r]&G' \ar[r]^f&
G \ar[r]^g&
G''\ar[r] &1\\
1\ar[r...
...varphi}&
G \ar[r]_-{\pi}\ar[u]\vert{\mathrm{id}}&
G/H\ar[r]\ar[u]\vert{\psi}&1}$](imagenes/img20.png)
 y
y 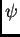 son isomorfismos.
son isomorfismos.
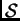 es una sucesión exacta con
es una sucesión exacta con 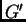 y
y 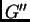 grupos
finitamente generados entonces
grupos
finitamente generados entonces 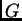 es finitamente generado.
es finitamente generado.
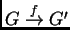 es un morfismo de grupos y
es un morfismo de grupos y
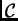 es una cadena abeliana (resp. cíclica) de
es una cadena abeliana (resp. cíclica) de 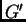 , entonces
, entonces
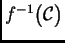 es una cadena abeliana (resp. cíclica)
de
es una cadena abeliana (resp. cíclica)
de 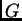 .
.
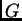 es un grupo y
es un grupo y 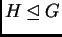 , entonces
, entonces 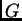 es
soluble (es decir,
es
soluble (es decir, 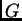 tiene una cadena abeliana con
tiene una cadena abeliana con 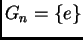 ) si
y sólo si
) si
y sólo si 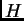 y
y 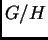 son solubles.
son solubles.