Tarea-Examen 3
Álgebra Moderna I
- Sea
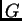 un grupo y
un grupo y 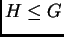 . Muestra que
. Muestra que 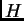 es normal en
es normal en 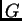 si y sólo si
si y sólo si 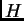 es unión de clases de conjugación de
es unión de clases de conjugación de 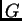 .
.
- Sea
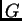 un grupo y
un grupo y 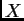 un
un 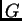 -conjunto. Si
-conjunto. Si 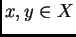 están en
la misma orbita, da un isomorfismo entre el estabilizador de
están en
la misma orbita, da un isomorfismo entre el estabilizador de 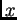 y el
estabilizador de
y el
estabilizador de 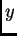 .
.
- Muestra que si
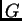 es un grupo finito y
es un grupo finito y 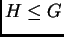 con
con ![$ [G:H]=p$](imagenes/img8.png) ,
donde
,
donde 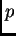 es el primo más pequeño que divide al orden de
es el primo más pequeño que divide al orden de 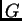 , entonces
, entonces
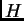 es normal en
es normal en 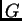 .
.
- Muestra que si
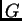 es un grupo finito de orden
es un grupo finito de orden 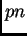 , donde
, donde 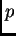 es
número primo mayor o igual que
es
número primo mayor o igual que  , entonces
, entonces 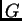 tiene un subgrupo
normal de orden
tiene un subgrupo
normal de orden 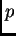 .
.
- Si
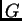 es grupo no abeliano de orden
es grupo no abeliano de orden 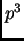 , muestra lo siguiente:
, muestra lo siguiente:
-
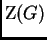 es cíclico de orden
es cíclico de orden 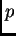 .
.
-
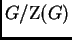 es isomorfo a
es isomorfo a
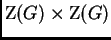 .
.
- Si
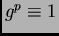 para todo
para todo 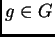 , entonces
, entonces 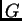 tiene un
subgrupo de orden
tiene un
subgrupo de orden 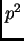 .
.
SUERTE!!!
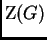 es cíclico de orden
es cíclico de orden 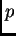 .
.
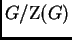 es isomorfo a
es isomorfo a
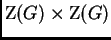 .
.
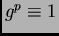 para todo
para todo 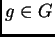 , entonces
, entonces 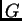 tiene un
subgrupo de orden
tiene un
subgrupo de orden 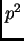 .
.