Axiomas de la Teoría de Conjuntos

Para intentar formalizar la Teoría de Conjuntos suupondremos que tenemos algunos objetos primitivos como números o letras y llamamos conjunto a una colección de objetos primitivos u otros conjuntos si ésta es construida a partir de los siguientes axiomas.

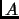
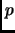
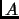
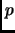
1   Esquema de Comprensión. Si $A$ es un conjunto y $p$ es una propiedad, la colección de los elementos en $A$ que cumplen la propiedad $p$ es un conjunto al que denotamos $\{a\in A\mid p(a)\}$.

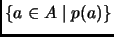
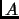
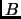
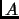
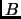
2   Axioma del Par. Si $A$ y $B$ son dos objetos, es decir, objetos primitivos o conjuntos, la colección que tiene por elementos a $A$ y $B$ es un conjunto al que denotamos $\{A,B\}$.

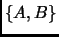
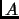
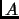
3   Axioma de la Unión. Si $A$ es un conjunto de conjuntos, es decir, un conjunto cuyos elementos son conjuntos, la colección cuyos elementos son los elementos de los elementos de $A$ es un conjunto al que denotamos $\bigcup A$.

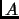
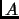
4   Axioma del Conjunto Potencia. Si $A$ es un conjunto, la colección que tiene por elementos a los subconjuntos de $A$ es un conjunto al que denotamos $\mathcal{P}(A)$.

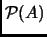
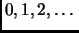
5   Axioma del Infinito La colección que tiene por elementos a los números naturales $0,1,2,\dots$ es un conjunto al que denotamos $\mathbb{N}$.

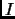
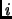
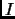
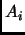
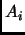
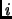
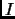
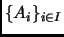
6   Axioma de Reemplazo. Si $I$ es un conjunto y para cada elemento $i$ de $I$ se tiene un conjunto $A_i$, la colección que tiene por elementos a los conjuntos $A_i$ para toda $i$ en $I$ es un conjunto al que denotamos $\{A_i\}_{i\in I}$ o $\{A_i\mid i\in I\}$.

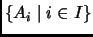
A los conjuntos construidos de esta manera los llamamos familias de conjuntos y al conjunto 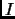$I$ lo llamamos el conjunto de índices de la familia.

Observa que dos conjuntos son iguales si y sólo si como colecciones son iguales, es decir, si y sólo si tienen los mismos elementos.

Definición 1   Si $A$ y $B$ son dos conjuntos, decimos que $A$ está contenido en $B$ y escribimos $A\subseteq B$ si todo elemento de $A$ es también un elemento de $B$.

En particular, dos conjuntos $A$ y $B$ son iguales si y sólo si $A$ está contenido en $B$ y $B$ está contenido en $A$.