 es reflexiva, es decir, para todo
es reflexiva, es decir, para todo 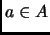 se tiene
que
se tiene
que 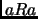 .
.
 es simétrica, es decir, si
es simétrica, es decir, si 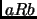 entonces
entonces 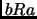 .
.
 es transitiva, es decir, si
es transitiva, es decir, si 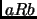 y
y 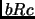 entonces
entonces
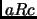 .
.
Ejemplos.
Entonces, ![]() es una relación de equivalencia en el conjunto de todos
los seres humanos.
es una relación de equivalencia en el conjunto de todos
los seres humanos.
Entonces, ![]() es una relación de equivalencia en el conjunto de los
números enteros. En este caso, si
es una relación de equivalencia en el conjunto de los
números enteros. En este caso, si ![]() es congruente con
es congruente con ![]() módulo
módulo
![]() , escribimos
, escribimos
![]() en lugar de
en lugar de
![]() .
.
Entonces, ![]() es una relación de equivalencia en el conjunto
de los números reales y
es una relación de equivalencia en el conjunto
de los números reales y
![]() si y sólo si la diferencia
de
si y sólo si la diferencia
de ![]() y
y ![]() es un entero.
es un entero.
Sea ![]() una relación de equivalencia en
una relación de equivalencia en ![]() . Si
. Si ![]() , definimos
la clase de equivalencia de
, definimos
la clase de equivalencia de ![]() módulo
módulo ![]() como el conjunto:
como el conjunto:
Tenemos entonces el siguiente resultado.
Ejemplos.
Observa que entonces, el conjunto de las clases de equivalencia de los
elementos de ![]() módulo
módulo ![]() puede identificarse con
puede identificarse con ![]() mismo.
mismo.
Tenemos entonces que todas las clases de equivalencia módulo ![]() son iguales, por lo que el conjunto de las clases de equivalencia
de los elementos de
son iguales, por lo que el conjunto de las clases de equivalencia
de los elementos de ![]() módulo la relación de equivalencia total
contiene un único elemento.
módulo la relación de equivalencia total
contiene un único elemento.
Tenemos entonces que el conjunto de las clases de equivalencia de los seres humanos módulo ésta relación puede identificarse con el conjunto de paises que existen.
Se puede observar entonces que si
![]() entonces
entonces
![]() y que cualquier otra clase de
equivalencia es igual a alguna de estas, es decir, existen exactamente
y que cualquier otra clase de
equivalencia es igual a alguna de estas, es decir, existen exactamente
![]() distintas clases de equivalencia módulo
distintas clases de equivalencia módulo ![]() ,
,
![]() .
.
Observese entonces que el conjunto de las clases de equivalencia de los números reales módulo esta relación puede identificarse con el círculo.