


Next: Funciones Inyectivas y Suprayectivas
Up: Relaciones
Previous: Composición de Relaciones y
Definición 8
Sea

una relación entre

y

. Decimos que

es una
función si para todo
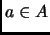
la imagen directa de
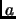
por

es un singulete, es decir,
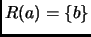
para algún
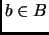
. En este
caso denotamos a
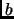
simplemente como
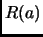
y lo llamamos
la
imagen de 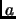 por
por 
.
Entonces,
Observa que si  es una relación entre
es una relación entre  y
y  , para que
, para que  sea
una función es necesario y suficiente que se cumplen las siguientes
dos condiciones:
sea
una función es necesario y suficiente que se cumplen las siguientes
dos condiciones:
- El dominio de
 es igual a
es igual a  ,
, 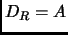 .
.
- Siempre que
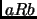 y
y 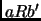 entonces
entonces 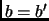 .
.
En general, a las relaciones que son funciones las denotamos con
letras minúsculas: 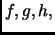 etc. y si
etc. y si 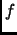 es una función entre
es una función entre  y
y
 decimos mejor que
decimos mejor que 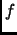 es una función de
es una función de  en
en  y
denotamos
y
denotamos
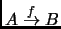 ; esto nos permite ver a una función
; esto nos permite ver a una función
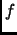 como una regla de asociación, que a cada elemento
como una regla de asociación, que a cada elemento 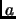 de
de
 asocian el elemento
asocian el elemento 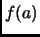 de
de  .
.
Notación 1
Observa que si

y

son dos conjuntos, el conjunto de todas
las relaciones entre

y

es igual al conjunto
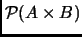
. Nosotros denotamos como
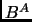
al subconjunto de
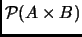
que tiene por elementos a las relaciones entre

y

que son funciones.
Ejemplos.
- Si
 es el conjunto de los alumnos en la clase de Álgebra
Superior, la regla que cada alumno en la clase asocia su edad puede
verse como una función de
es el conjunto de los alumnos en la clase de Álgebra
Superior, la regla que cada alumno en la clase asocia su edad puede
verse como una función de  en el conjunto de los números naturales,
en el conjunto de los números naturales,
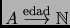 . Entonces,
. Entonces,
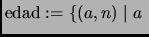
es un alumno de Álgebra Superior
con
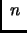
años de edad
- Si
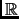 denota el conjunto de los números reales, la regla que a
cada número real
denota el conjunto de los números reales, la regla que a
cada número real 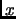 asocia su cuadrado
asocia su cuadrado 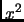 puede verse como una
función de
puede verse como una
función de
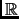 en
en
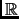 ,
,
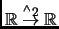 .
Entonces,
.
Entonces,
La forma en como se comportan los conceptos de composición de
relaciones y relación inversa en el contexto de funciones, puede verse
en el siguiente Teorema y la siguiente Definición.
Teorema 9
Sea
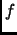
una relación entre

y

, y
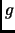
una relación entre

y
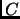
. Entonces, si
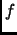
y
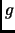
son funciones la relación composición
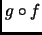
también es una función, en este caso
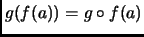
para toda
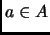
.
Definición 10
Si
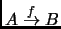
es una función, decimos que
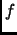 es
biyectiva o invertible
es
biyectiva o invertible si
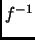
, la relación inversa de
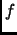
,
también es una función.
Observa que si
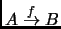 es una función, para que
es una función, para que 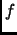 sea
biyectiva es necesario y suficiente que la imagen inversa de cualquier
sea
biyectiva es necesario y suficiente que la imagen inversa de cualquier
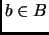 sea un singulete, es decir,
sea un singulete, es decir,
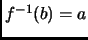 para alguna
para alguna
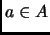 . Entonces,
. Entonces, 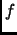 es biyectiva si y sólo si para todo
es biyectiva si y sólo si para todo 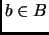 existe un único
existe un único 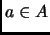 tal que
tal que 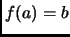 .
.



Next: Funciones Inyectivas y Suprayectivas
Up: Relaciones
Previous: Composición de Relaciones y
Elhoim Sumano (CP)
2003-01-20
![]() es una relación entre
es una relación entre ![]() y
y ![]() , para que
, para que ![]() sea
una función es necesario y suficiente que se cumplen las siguientes
dos condiciones:
sea
una función es necesario y suficiente que se cumplen las siguientes
dos condiciones:
![]() etc. y si
etc. y si ![]() es una función entre
es una función entre ![]() y
y
![]() decimos mejor que
decimos mejor que ![]() es una función de
es una función de ![]() en
en ![]() y
denotamos
y
denotamos
![]() ; esto nos permite ver a una función
; esto nos permite ver a una función
![]() como una regla de asociación, que a cada elemento
como una regla de asociación, que a cada elemento ![]() de
de
![]() asocian el elemento
asocian el elemento ![]() de
de ![]() .
.
![]() es una función, para que
es una función, para que ![]() sea
biyectiva es necesario y suficiente que la imagen inversa de cualquier
sea
biyectiva es necesario y suficiente que la imagen inversa de cualquier
![]() sea un singulete, es decir,
sea un singulete, es decir,
![]() para alguna
para alguna
![]() . Entonces,
. Entonces, ![]() es biyectiva si y sólo si para todo
es biyectiva si y sólo si para todo ![]() existe un único
existe un único ![]() tal que
tal que ![]() .
.