Funciones Inyectivas y Suprayectivas

Definición 11   Sea $A\stackrel{f}{\to}B$ una función.

1. Decimos que 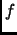$f$ es una función inyectiva si siempre que 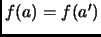$f(a)=f(a')$ entonces $a=a'$.
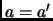2. Decimos que 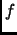$f$ es una función suprayectiva si para todo 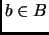$b\in B$ existe al menos una 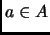$a\in A$ tal que $f(a)=b$.

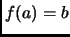Puede verse entonces que si $f$ es una función, $f$ es biyectiva si y sólo si $f$ es inyectiva y suprayectiva.

Los siguientes Teoremas caracterizan de un modo simétrico a las funciones que son inyectivas y a las que son suprayectivas.

Teorema 12   Si $A\stackrel{f}{\to}B$ es una función, son equivalentes:

1. $f$ es inyectiva.
2. $f^{-1}\circ f=\mathrm{id}_A$
3. Existe una relación $R$ entre $B$ y $A$ tal que $R\circ f=\mathrm{id}_A$.
4. Si $S$ y $S'$ son dos relaciones entre cualquier conjunto $C$ y $A$ tales que $f\circ S=f\circ S'$, entonces $S=S'$.
5. Para todo $\Omega\subseteq A$ se tiene que $f^{-1}(f(\Omega))=\Omega$.

Teorema 13   Si $A\stackrel{f}{\to}B$ es una función, son equivalentes:

1. $f$ es suprayectiva.
2. $f\circ f^{-1}=\mathrm{id}_B$
3. Existe una relación $R$ entre $B$ y $A$ tal que $f\circ R=\mathrm{id}_B$.
4. Si $S$ y $S'$ son dos relaciones entre $B$ y cualquier conunto $C$ tales que $S\circ f=S'\circ f$, entonces $S=S'$.
5. Para todo $\Omega\subseteq B$ se tiene que $f(f^{-1}(\Omega))=\Omega$.