-
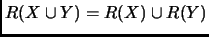
-
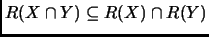
-
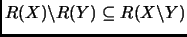
- Da un ejemplo de que las igualdades en los incison (b) y (c) no siempre se cumplen.
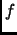 es biyectiva, es decir, la relación
es biyectiva, es decir, la relación 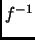 es una función.
es una función.
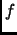 es inyectiva y suprayectiva.
es inyectiva y suprayectiva.
- Existe una función
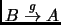 tal
que
tal
que
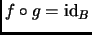 y
y
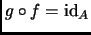 .
.
- Si
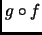 es inyectiva entonces
es inyectiva entonces 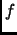 es inyectiva.
es inyectiva.
- Si
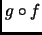 es suprayectiva entonces
es suprayectiva entonces 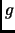 es suprayectiva.
es suprayectiva.
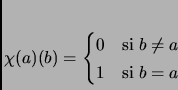
Prueba que ![]() es una función inyectiva.
es una función inyectiva.
Más generalmente, con las mismas consideraciones
define la función
![]() que a cada elemento
que a cada elemento
![]() asocia la función
asocia la función
![]() llamada función caracteristica de
llamada función caracteristica de ![]() y definida como:
y definida como:
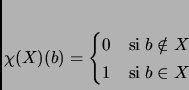
Prueba que ![]() también una función inyectiva.
también una función inyectiva.
y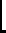
¿Son ![]() y
y ![]() reflexivas, simétricas o transitivas?. Explica.
reflexivas, simétricas o transitivas?. Explica.
 es reflexiva si y sólo si
es reflexiva si y sólo si
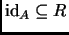 .
.
 es simétrica si y sólo si
es simétrica si y sólo si 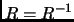 .
.
 es transitiva si y sólo si
es transitiva si y sólo si
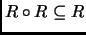 .
.
 es reflexiva y transitiva si y sólo si
es reflexiva y transitiva si y sólo si
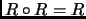 y
y
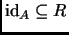 .
.
- Satisfagan dos de las tres condiciones reflexiva, simétrica y transitiva, pero no la tercera.
- Satisfagan una de las tres condiciones reflexiva, simétrica y transitiva pero no las otras dos.
- No satisfagan ninguna de las condiciones reflexiva, simétrica y transitiva.