Particiones

Definición 16   Si $A$ es un conjunto, una partición $\Omega$ de $A$ es una familia de subconjuntos no vaciós tales que:

1. Los elementos de 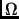$\Omega$ son ajenos, es decir, si 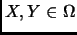$X,Y\in \Omega$ entonces 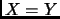$X=Y$ o $X\cap Y=\emptyset$.
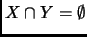2. Los elementos de 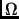$\Omega$ cubren al conjunto $A$, es decir, $\bigcup \Omega =A$.

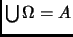Sea $A$ un conjunto. Si $R$ es una relación de equivalencia en $A$, por el Teorema 15 el conjunto de las clases de equivalencia de los elementos de $A$ módulo $R$, $\{[a]_R\mid a\in A\}$, es una partición de $A$. Esto nos define una función:

$$\xy(0,-3)*={},*+<3.2cm,1.2cm>{}*\frm{... ... \text{Particiones} \\ \text{equivalencia en $A$}&&&&&&&\text{en $A$}} \endxy$$

donde $f(R)=\{[a]_R\mid a\in A\}$.

Teorema 17   Si $A$ es un conjunto, la función $f$ de arriba es una biyección.

Proof. Define la función

$$\xy(0,-3)*={},*+<3.2cm,1.2cm>{}*\frm{... ... \text{Particiones} \\ \text{equivalencia en $A$}&&&&&&&\text{en $A$}} \endxy$$

de la siguiente manera

$$g(\Omega):=\{(a,b)\in A\times A \mid$$   existe$$\;X\in\Omega\;$$tal que$$\;a,b\in X\}$$

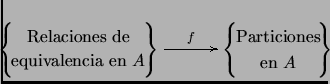
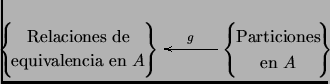
Queda como ejercicio ver que $g(\Omega)$ es una relación de equivalencia en $A$ si $\Omega$ es una partición en $A$ y que las igualdades $f\circ g=\mathrm{id}$ y $g\circ f=\mathrm{id}$ se cumplen.

Concluimos entonces del Ejercicio 3 que $f$ es una biyección. $\qedsymbol$