

Next: Representation theory of algebras
Up: Cluster algebras and related
Previous: Geometry
Kontsevich and Soibelman have discovered tantalizing links between
cluster algebras, stability conditions [19] and Donaldson-Thomas
invariants. Large parts of their theory are still conjectural but a
fascinating overall picture is already emerging. In their
construction, they start from a quiver (without loops or 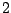 -cycles)
endowed with a superpotential and associate to it a
-cycles)
endowed with a superpotential and associate to it a 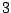 -Calabi-Yau
triangulated category
-Calabi-Yau
triangulated category 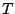 with a
with a 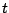 -structure. They then define and
study a refinement of Bridgeland's space of stability conditions on
-structure. They then define and
study a refinement of Bridgeland's space of stability conditions on
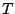 (or more generally on any
(or more generally on any 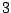 -Calabi-Yau category with
ind-constructible moduli stacks of objects and morphisms). They
define abstract Donaldson-Thomas invariants using their putative
generating functions on the space of stability conditions, see for example
the note [80].
Cluster transformations then govern the way these generating functions
behave under wall-crossing in the space of stability conditions.
-Calabi-Yau category with
ind-constructible moduli stacks of objects and morphisms). They
define abstract Donaldson-Thomas invariants using their putative
generating functions on the space of stability conditions, see for example
the note [80].
Cluster transformations then govern the way these generating functions
behave under wall-crossing in the space of stability conditions.


Next: Representation theory of algebras
Up: Cluster algebras and related
Previous: Geometry
![]()
![]()
![]()