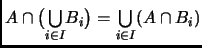Next: About this document ...
Up: Teoría de Conjuntos
Previous: Uniones e Intersecciones de
- Demuestra que si
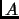 es un conjunto, la colección de todos los
objetos que no son elementos de
es un conjunto, la colección de todos los
objetos que no son elementos de 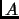 no es un conjunto.
no es un conjunto.
-
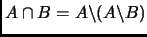 .
.
- Si
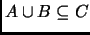 , entonces
, entonces
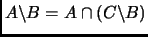 .
.
-
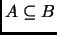 si y sólo si para todo conjunto
si y sólo si para todo conjunto 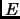 ,
,
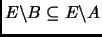 .
.
-
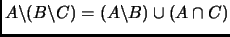 .
.
- Muestra por medio de ejemplos que las siguientes proposiciones
son falsas:
-
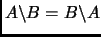 .
.
- Si
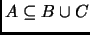 entonces
entonces
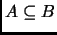 o
o
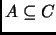 .
.
- Definimos la diferencia simétrica de
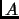 y
y 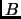 como el
conjunto
como el
conjunto
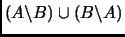 y lo denotamos por
y lo denotamos por
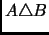 . Demuestra que:
. Demuestra que:
-
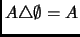 .
.
-
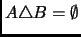 si y sólo si
si y sólo si 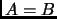 .
.
- Si
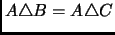 , entonces
, entonces 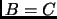 .
.
-
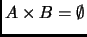 si y sólo si
si y sólo si
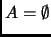 o
o
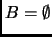 .
.
-
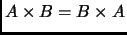 si y sólo si
si y sólo si 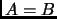 .
.
-
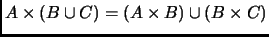 .
.
-
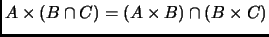 .
.
- Usando las leyes de De Morgan y el ejercicio 4 enuncia y
demuestra las igualdades duales de los siguientes enunciados:
-
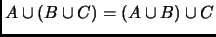 .
.
-
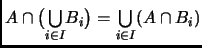
-
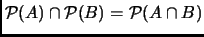
-
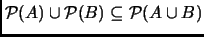
- Muestra con un ejemplo que la igualdad en el ejercicio 14 no
siempre se cumple.
Elhoim Sumano (CP)
2002-12-11
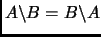 .
.
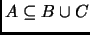 entonces
entonces
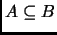 o
o
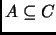 .
.
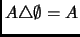 .
.
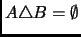 si y sólo si
si y sólo si 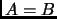 .
.
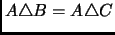 , entonces
, entonces 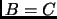 .
.
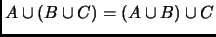 .
.