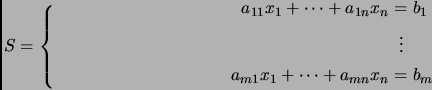 |
(1) |
Cuando tenemos un sistema como este, queremos encontrar su
conjunto de soluciones, es decir, el conjunto de ![]() -ádas de números
reales
-ádas de números
reales
![]() tales que las igualdades de
(1) se cumplen.
tales que las igualdades de
(1) se cumplen.
Si el sistema de ecuaciones lineales es de la forma
Por último, basados en la creencia de que el conjunto de soluciones del sistema (2) es igual al conjunto de soluciones del sistema (3), encontramos el conjunto de soluciones de (2) sustituyendo la segunda ecuación de (3) en la primera. Así, llegamos a lo siguiente:
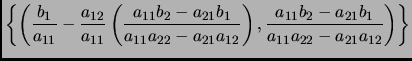
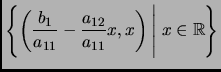
Para intentar extender este método a sistemas de ecuaciones lineales arbitrarios, es conveniente ver a un sistema de ecuaciones desde un punto vista matricial.
Recordemos primero que una matriz de ![]() es un arreglo
de la forma:
es un arreglo
de la forma:
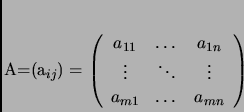
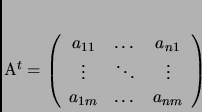
También, si
![]() y
y
![]() son dos matrices de
son dos matrices de ![]() y de
y de ![]() respectivamente, entonces el producto
respectivamente, entonces el producto ![]() se define como la
matriz de
se define como la
matriz de ![]() que tiene en su
que tiene en su ![]() -ésima entrada a la suma
-ésima entrada a la suma
![]() .
.
Con esta notación, un sistema de ![]() ecuaciones lineales en
ecuaciones lineales en ![]() incógnitas como (1) puede verse como una pareja ordenada
incógnitas como (1) puede verse como una pareja ordenada
![]() donde
donde
![]() es una matriz de
es una matriz de ![]() llamada
la matriz de coeficientes del sistema y
llamada
la matriz de coeficientes del sistema y ![]() es una matriz
de
es una matriz
de ![]() .
.
De este modo, el conjunto de soluciones del sistema ![]() es igual
al conjunto
es igual
al conjunto

Notemos ahora que si
![]() denota a la matriz elemental
de
denota a la matriz elemental
de ![]() con
con ![]() -ésima entrada igual a
-ésima entrada igual a ![]() , es decir, la
matriz de
, es decir, la
matriz de ![]() que tiene
que tiene ![]() 's en la diagonal,
's en la diagonal, ![]() en la
en la
![]() -ésima entrada y ceros en las entradas restantes, entonces:
-ésima entrada y ceros en las entradas restantes, entonces:
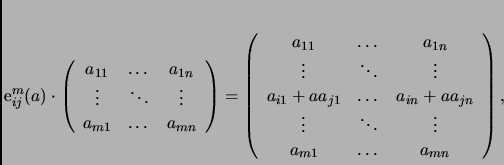
Podemos ver entonces que nuestra creencia para resolver un sistema de
![]() ecuaciones lineales en
ecuaciones lineales en ![]() incógnitas está sustentado en el
siguiente Teorema.
incógnitas está sustentado en el
siguiente Teorema.
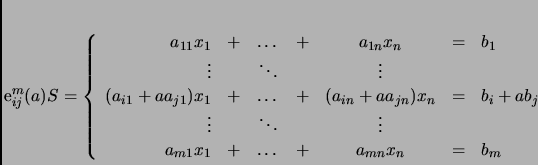
La prueba de este Teorema se sigue inmediatamente del siguiente Lema.
El método con el que encontramos las soluciones de un sistema de ![]() ecuaciones lineales en
ecuaciones lineales en ![]() incógnitas se generaliza al siguiente
Teorema.
incógnitas se generaliza al siguiente
Teorema.
 |
(4) |
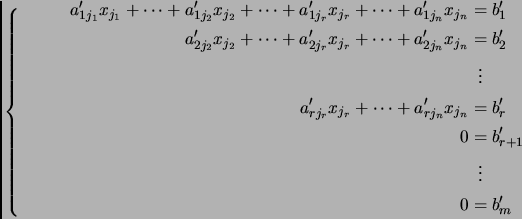 |
(5) |