


Next: Funciones
Up: Relaciones
Previous: Imágenes Directas e Inversas
Definición 3
Si

es una relación entre

y

, y
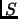
es una relación entre

y
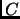
, definimos la
composición de  y
y 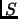
como la
siguiente relación entre

y
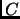
:
Notemos que la composición de relaciones en general no puede ser
conmutativa, es decir,
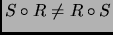 . Sin embargo, sí es
asociativa:
. Sin embargo, sí es
asociativa:
Teorema 4
Si

es una relación entre

y

,
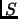
una relación entre

y
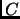
, y
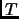
una relación entre
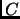
y
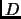
, entonces
Definición 5
Si

es una relación entre

y

, definimos la
inversa de

como la siguiente relación entre

y

:
Notemos que si 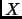 es un subconjunto de
es un subconjunto de  , entonces la imagen
directa de
, entonces la imagen
directa de 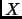 por
por  es igual a la imagen inversa de
es igual a la imagen inversa de 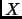 por
por
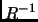 , es decir,
, es decir,
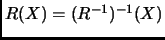 . También, si
. También, si 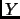 es un
subconjunto de
es un
subconjunto de  , la imagen inversa de
, la imagen inversa de 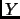 por
por  es igual a la
imagen directa de
es igual a la
imagen directa de 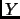 por
por 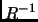 , así que no hay confusión con la
notación
, así que no hay confusión con la
notación 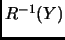 .
.
Daremos ahora dos teoremas que relacionan los conceptos de
composición de relaciones y de relación inversa.
Teorema 6
La relación inversa de una composición de relaciones es igual a la
composición inversa de las relaciones inversas, es decir,
si

es una relación entre

y

, y
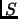
una relación entre

y
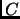
, entonces
Teorema 7
Si

es una relación entre

y

, entonces
-
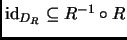 .
.
-
 .
.



Next: Funciones
Up: Relaciones
Previous: Imágenes Directas e Inversas
Elhoim Sumano (CP)
2003-01-20
![]() . Sin embargo, sí es
asociativa:
. Sin embargo, sí es
asociativa:
![]() es un subconjunto de
es un subconjunto de ![]() , entonces la imagen
directa de
, entonces la imagen
directa de ![]() por
por ![]() es igual a la imagen inversa de
es igual a la imagen inversa de ![]() por
por
![]() , es decir,
, es decir,
![]() . También, si
. También, si ![]() es un
subconjunto de
es un
subconjunto de ![]() , la imagen inversa de
, la imagen inversa de ![]() por
por ![]() es igual a la
imagen directa de
es igual a la
imagen directa de ![]() por
por ![]() , así que no hay confusión con la
notación
, así que no hay confusión con la
notación ![]() .
.