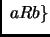Divisibilidad en
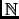 .
Si
.
Si 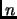 es un número natural, la imagen directa de
es un número natural, la imagen directa de 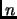 por la relación
de divisibilidad
por la relación
de divisibilidad 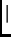 es igual al conjunto de los números naturales
que son múltiplos de
es igual al conjunto de los números naturales
que son múltiplos de 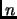 :
:
Del mismo modo, si 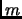 es un número natural, la imagen inversa de
es un número natural, la imagen inversa de 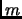 por la relación de divisibilidad
por la relación de divisibilidad 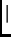 es igual al conjunto de los
números naturales que dividen a
es igual al conjunto de los
números naturales que dividen a 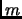 :
:
Por ejemplo, puede mostrarse fácilmente que todo número natural divide
al 0, es decir,
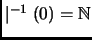 y que solamente el
y que solamente el 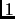 divide al
divide al
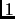 , es decir,
, es decir,
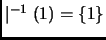 .
.
También, puede mostrarse que si 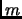 es cualquier número natural
diferente de 0, entonces
es cualquier número natural
diferente de 0, entonces
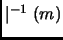 es un conjunto que tiene un
número finito de elementos, entre los que siempre se encuentran el
es un conjunto que tiene un
número finito de elementos, entre los que siempre se encuentran el 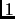 y
y 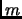 pero nunca el 0.
pero nunca el 0.
Decimos que un número natural 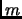 es primo si
es primo si
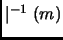 es un conjunto con exactamente dos elementos. Entonces,
es un conjunto con exactamente dos elementos. Entonces,
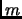 es primo si y sólo si
es primo si y sólo si 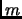 es diferente de
es diferente de 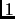 y
y
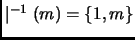
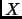 es un subconjunto de
es un subconjunto de  denotamos como
denotamos como 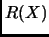 a
la imagen directa de
a
la imagen directa de 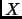 por
por  definida como el conjunto de
los elementos
definida como el conjunto de
los elementos 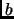 de
de  con la propiedad de que existe
con la propiedad de que existe 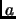 en
en 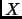 tal que
tal que 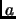 está
está  -relacionada con
-relacionada con 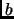 , es decir,
, es decir,
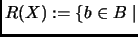 existe
existe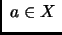 tal que
tal que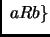
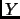 es un subconjunto de
es un subconjunto de  denotamos como
denotamos como 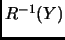 a
la imagen inversa de
a
la imagen inversa de 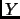 por
por  definida como el conjunto de
los elementos
definida como el conjunto de
los elementos 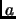 de
de  con la propiedad de que existe
con la propiedad de que existe 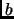 en
en 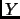 tal que
tal que 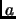 está
está  -relacionada con
-relacionada con 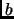 , es decir,
, es decir,
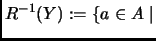 existe
existe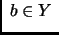 tal que
tal que