|
Pasos para mostrar que la proyección estereográfica es conforme |
|||||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Todo
lo que viene podemos visualizar completamente en el plano
![]() ,
es decir reducimos el problema en el espacio a un problema en el plano.
En este plano
,
es decir reducimos el problema en el espacio a un problema en el plano.
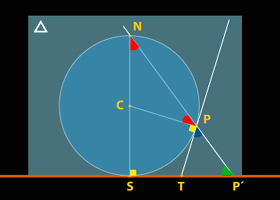
En este plano ![]() encontramos los siguientes
puntos: el centro de la proyección N,
el centro de la tierra C,
un punto sobre la tierra P, su proyección
P',
el punto S, opuesto
a N y el punto T.
encontramos los siguientes
puntos: el centro de la proyección N,
el centro de la tierra C,
un punto sobre la tierra P, su proyección
P',
el punto S, opuesto
a N y el punto T.
Pero de los planos tangentes sólo vemos líneas: la recta PT y la recta P'S que se intersectan en T. Como P y N se encuentran en la superficie de la tierra (que vemos como una circunferencia), tienen la misma distancia del centro C: el triángulo NCP es isósceles y de ahí que el ángulo NPC es igual al ángulo PNC (los dos ángulos rojos), usando el teorema B).
Como PT y SP' son tangentes a la tierra tenemos que los ángulos CPT y CSP' son ángulos rectos (amarrrillos en el dibujo). Si nos fijamos en el triángulo NSP' entonces este tiene tres ángulos: rojo , amarrillo y uno tercero en verde. Estos tres ángulos suman 180 grados, porque la suma de los ángulos en cualquier triángulo es 180 grados. Por otro lado, el ángulo NPP' mide también 180 grados (es dif’cil verlo como un ángulo), podemos verlo como la suma de un ángulo rojo con amarrillo y uno tercero en azul. Pero como rojo+amarrillo +azul=180 grados y rojo+amarrillo+azul=180 grados obtenemos que azul=verde. Usando el teorema C), obtenemos que los dos lados PT y P'T son iguales. Esto es lo que teníamos que demostrar.