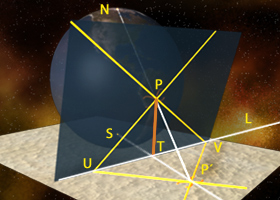
Lo que habrá que demostrar es que el ángulo UPV es igual al ángulo UP'V . Se dibuja adicionalmente el segmento P'S y se donta con T al punto de intersección de este segmento con la recta l. La demostración se parte en dos "pasos", o dos fases. En el primer paso se muestra que es suficiente mostrar que el segmento PT es igual de largo que P'T, es decir se muestra que una vez que se sabe que PT=P'T, entonces se puede concluir que los dos ángulos UPV y UP'V son iguales.

En el segundo paso se muestra que en efecto se tiene PT=P'T. En el primer paso sólo se asume que PT=P'T , y se concluye que de ahí se sigue el resultado buscado, mientras en el segundo paso se muestra la veracidad de PT=P'T.

Tiene algo de artificial hacer la demostración en este orden, porque con la misma certez matemática se podría hacer primero el paso dos y luego el paso uno. Pero este orden tiene la desventaja que el primer paso parece mal motivado: aparentemente no tiene nada que ver con el problema original. Así en el orden propuesto, se muestra primero por qué es interesante compara las longitudes de PT y de P'T .