Un nuevo enfoque a la ecuación de los círculos en el plano
Institución: CIMAT
Tipo de Evento: Investigación, Divulgación
| Cuándo |
11/10/2022 de 12:00 a 13:00 |
|---|---|
| Dónde | Auditorio "Alfonso Nápoles Gándara" |
| Agregar evento al calendario |
|
La ecuación de los círculos en el plano es \(x^2 + y^2 = r^2\), con \(x\) e \(y\) números reales. Si ampliamos el cuerpo de números que estamos considerando de los reales a los complejos, la misma ecuación nos determina otro conjunto \(S(r)\), que es ahora una superficie bidimensional.
De manera natural, veremos que esta superficie que vive en \(\mathbb{R}^4 = \mathbb{C}^2\) está formada por la unión de círculos (como una cebra en el zoológico) y de hecho tiene un círculo central remarcable.
Si proyectamos \(S(r)\) a la primera o segunda variable de \(\mathbb{C}^2\), estos círculos se convierten en dos familias de elipses disjuntas que forman el plano \(\mathbb{C}\) . Estas elipses tienen una parametrización natural y son enviadas una en la otra via la ecuación \(x^2+y^2=r^2\).
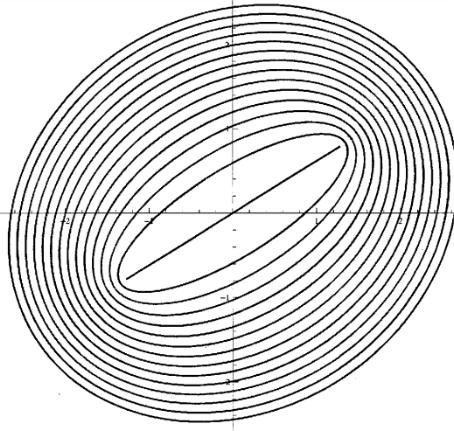
Por otro lado si proyectamos \(S(r)\) a la parte real o a la parte imaginaria, estos círculos son círculos en el plano, pero con un radio mayor que uno específico en cada plano real, que son enviadas una en la otra via la ecuación \(x^2 + y^2=r^2\) preservando una parametrización natural.
Estos resultados se transparentan al considerar las variables complejas \(x_1 + ix_2\) y \(y_1 + iy_2\) por un lado y las variables complejas \(x_1 + iy_1\) y \(x_2 + iy_2\) en el mismo \(\mathbb{R}^4\), así como las acciones del círculo \(S^1\) de los números complejos de norma 1.
Veremos al final cómo estos resultados se pueden generalizar a otras ecuaciones vía el mapeo de Gauss (la matriz jacobiana), donde al cortar la superficie en los "círculos remarcables" nos dan información de cómo se organizan las singularidades de la ecuación.

